The question about how recursion works is among the most frequently asked ones in Codecademy Forums for exercises such as this one. This text will walk you through what happens in your JavaScript when a recursive function is called.

How to read the diagrams

To understand the diagrams that you see below, please read this article. It will also provide you with a basic understanding of what happens in the computer when a function calls "itself".
In short: a diagram like this...

...represents the fact that the function square, when called with the argument 7 (like this: square(7)) will return the number 49. The function itself is most probably defined as:

function square(n) { return n * n }

So, if we wanted to visualize on a deeper level of detail what happens inside this function when it is called with the argument 7, we'd do this:

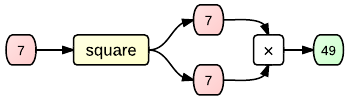
As you can see, a function's return value is represented by the single green node that all paths which diverge from a function lead to (because every function in JavaScript only has one return value).

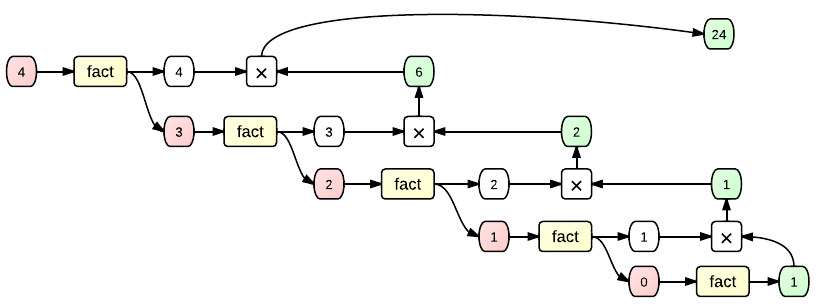
Recursive Factorial

An often-cited example of a recursive function is the one that uses recursion to calculate the factorial of a natural number. Wikipedia provides the following recursive definition of the factorial:

See the word "if" there? There are some comparison expressions like n>0 as well… actually, this formal mathematical definition translates into the actual working code in a programming language (let's say JavaScript) in a straightforward way: we just use the JavaScript syntax for the if construct, and we write fact(n) instead of n! ("fact" is short for "factorial", of course), to get this:

function fact(n) {
    if ( n === 0 ) return 1;
    if ( n  >  0 ) return n * fact( n - 1 );
}

Now it's obvious that if we call this function with a 0 as argument, the first if condition will fire, and it'll return 1. Boring but essential! Because this is the so-called base case, the one that the recursion must eventually reach in order to terminate. So what happens when the input argument is larger than zero, as in fact(4), for instance?

Before I present you with my fancy diagram, let's use a more text-based approach first (or, math-based if you will). You can think of a function as a simple device that rewrites expressions. You've all seen this in Math class at least a hundred times:

x = (5)² + 1
x = 25   + 1

The only difference between the first and the second line is that (5)² was rewritten as 25, which is simply the result of applying the square function ()² to the value 5. Translate that into JavaScript, and you have, as above:

function square(n) { return n * n }
square(5);
5 * 5;

It doesn't matter if you write square(5) or 5 * 5 at that point, they're absolutely equivalent. So wherever we use the former, we can use the latter instead (just as we can interchangeably use (5)² and 25 – they're the same). The function that we used just stupidly rewrites things for us. And we can easily do the rewriting ourselves using pencil and paper: let's assume we have the function given above and the line square(5). To obtain the result, we do this:

1. replace square(5) by what the square method returns (i.e. everything after the return keyword)
2. since it was square(5) and not square(n), replace every n by 5
3. You're done!

In JavaScript code:

square(5)      // function call
n * n          // replaced by what is returned
5 * 5          // n replaced by actual argument
25             // simplifying, done!

We can apply the exact same technique to the factorial function now, calling it with the argument 4, now doing the replacements and simplifications all in one step. There are only two differences between fact() and the simpler square method above:

• square() always does the same kind of rewriting, while for fact() it depends on the input value
• unlike square(), fact() can call fact() internally because it is recursive

So let's try and rewrite this stuff, shall we? We will simplify obvious arithmetic expressions: 4-1 equals 3, so we will just use 3 on the next line.

  fact(4)                         // 4 > 0
= 4 * fact(4-1)                   // 4-1 = 3 > 0
= 4 * 3 * fact(3-1)               // 3-1 = 2 > 0
= 4 * 3 * 2 * fact(2-1)           // 2-1 = 1 > 0
= 4 * 3 * 2 * 1 * fact(1-1)       // 1-1 = 0 equals 0 --> return 1
= 4 * 3 * 2 * 1 * 1
= 24

You see, when we're acting like we're the computer, all we need to do is rewrite expressions! In the lines above, when stuff2 is immediately below stuff1, it means that stiff1 was rewritten with the result being stuff2, and the rewriting is justified by the fact that both are absolutely equivalent.

Now let's have a look at the same thing as a diagram: